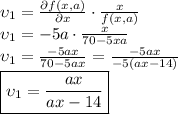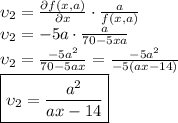Answer:
a) The x value of the point where the two equations intersect in terms of a is
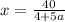
b) The value of the functions at the point where they intersect is
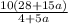
c) The partial derivative of f with respect to
 is
is
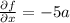 and the partial derivative of f with respect to
and the partial derivative of f with respect to
 is
is
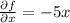
d) The value of
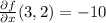 and
and

e)
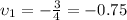 and
and
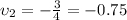
f) equation
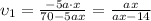 and
and
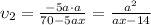
Explanation:
a) In order to find the
 we just need to equal the equations and solve for
we just need to equal the equations and solve for
 :
:

b) Since we need to find the value of the function in the intersection point we just need to substitute the result from a) in one of the functions. As a sanity check , I will do it in both and the value (in terms of
 ) must be the same.
) must be the same.
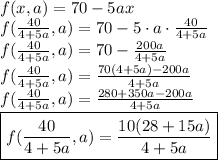
and for
 :
:
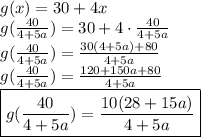
c)
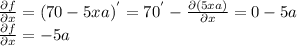
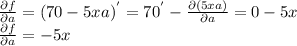
d) Then evaluating:
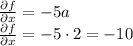
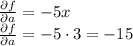
e) Substituting the corresponding values:
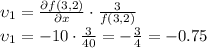
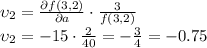
f) Writing the equations: