Question

Use De Morgan's Law to negate the following statements. a. Vx(x >5) b. 3.(x2+2x + 1 = 0)

Answer 1

a)
`\\eg \forall x :x>5 \equiv \forall x:x\leq 5`

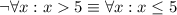
b)
`\\eg [x^2+2x+1=0]\equiv x^2+2x+1\\eq0` or the set
`\{x:x\\eq-1\}`

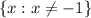
Explanation:

First, notice that in both cases we have to sets:

a) is the set of all real numbers which are higher than 5 and in

b) the set is the solution of the equation
`x^2+2x+1=0` which is the set
`x=-1`

De Morgan's Law for set states:

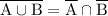`\overline{\rm{A\cup B}} = \overline{\rm{A}} \cap \overline{\rm{B}}\\`, being
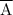`\overline{\rm{A}}` and
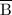`\overline{\rm{B}}` are the complements of the sets
`A` and
`B`.
`\cup` is the union operation and
`\cap` the intersection.

Thus for:

a)
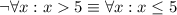`\\eg \forall x :x>5 \equiv \forall x:x\leq 5`. Notice that
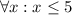`\forall x:x\leq 5` is the complement of the given set.

b)
`\\eg [x^2+2x+1=0]\equiv x^2+2x+1\\eq0` which is the set
`B = \{x:x\\eq-1\}`