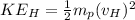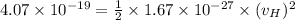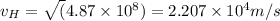Answer:
The recoil speed is
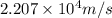
Solution:
Wavelength of a blue-green photon,
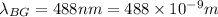
Now, the energy associated with the blue-green photon:
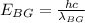
where
h = Planck's constant
C = speed of light ion vacuum
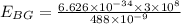
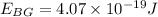
Also, we know that the recoil speed can be calculated by the KInetic energy which is equal to the Energy of the blue-green photon:
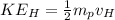
where
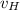 = velocity of Hydrogen atom
= velocity of Hydrogen atom
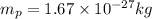 = mass of H-atom
= mass of H-atom
Now,