Question

In a TV set, an electron beam moves with horizontal velocity of 4.3 x 10^7 m/s across the cathode ray tube and strikes the screen, 43 cm away. The acceleration of gravity is 9.8 m/s^2. How far does the electron beam fall while traversing this distance? Answer in units of m

Answer 1

`y=-4.9x10^(-16)m`

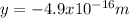
Step-by-step explanation:

From the exercise we have initial velocity on the x-axis, the final x distance and acceleration of gravity.

`v_(ox)=4.3x10^(7)m/s`

`x=43cm=0.43m\\g=9.8m/s^(2)`

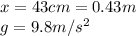
From the equation on moving particles we can find how long does it take the electron beam to strike the screen

`x=x_(o)+v_(ox)t+(1)/(2)at^(2)`

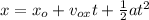
Since
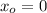`x_(o)=0` and
`a_(x)=0`

`0.43m=(4.3x10^(7)m/s)t`

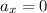
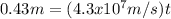
Solving for t

`t=1x10^(-8) s`

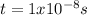
Now, from the equation of free-falling objects we can find how far does the electron beam fell

`y=y_(o)+v_(oy)t+(1)/(2)gt^(2)`

`y=-(1)/(2)(9.8m/s^(2))(1x10^(-8) s)=-4.9x10^(-16)m`

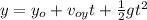
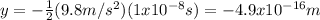
The negative sign means that the electron beam fell from its initial point.