Answer:
Use the formula

Explanation:
Let
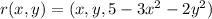 be the explicit parametrization of the paraboid. The intersection of this paraboid with the xy plane is the ellipse given by
be the explicit parametrization of the paraboid. The intersection of this paraboid with the xy plane is the ellipse given by
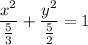
The partial derivatives of the parametrization are:
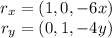
and computing the cross product we have
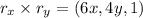 . Then
. Then
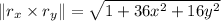
Then, if
 is the interior region of the ellipse the superficial area located above of the xy is given by the double integral
is the interior region of the ellipse the superficial area located above of the xy is given by the double integral

The last integral is not easy to calculate because it is an elliptic integral, but with any software of mathematics you can obtain this value.