Question

A thin copper rod of mass = 100 g is forced to rotate about a horizontal axis passing through one end. if the road is released from rest and the angular speed at its lowest position is 7rad/sec, what is the length of the rod?

Answer 1

The length of the rod is 0.6 m

Solution:

Mass of the copper rod, m = 100 g = 0.1 kg

Angular speed at lowest position,
`\omega_(L) = 7 rad/s`

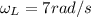
Now,

By using the law of conservation of energy, the overall mechanical energy of the system taken about the center of mass remain conserve.

Thus at the initial position of the rod, i.e., horizontal:

`(1)/(2)mv_(c)^(2) + (1)/(2)I\omega^(2) + mg(L)/(2) =0 + mg(L)/(2)`

`(1)/(2)mv_(c)^(2) + (1)/(2)I\omega^(2) = 0`

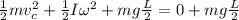
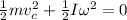
(Since,
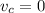`v_(c) = 0` and
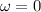`\omega = 0` at horizontal position).

where

Tranlational Kinetic energy about center of mass =
`(1)/(2)mv_(c)^(2)`

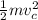
Rotational K.E about the center of mass,
`(1)/(2)I\omega^(2)`

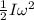
Potential energy about Center of Mass =
`mg(L)/(2)`

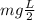
Now, applying the law of conservation at the lowest point of the rod:

`(1)/(2)mv'_(c)^(2) + (1)/(2)I\omega'^(2) + 0 =(1)/(2)m((\omega' L)/(2))^(2) + (1)/(2)I\omega'^(2)`

`(1)/(2)mv'_(c)^(2) + (1)/(2)I\omega'^(2)  =(1)/(2)m((\omega' L)/(2))^(2) + (1)/(2)(mL^(12))/(12)\omega'^(2) = (mL^(2)\omega'^(2))/(6)`

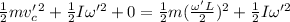
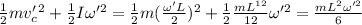
where

Moment of inertia about the center of mass at the lowest position is
`(mL^(2))/(12)`

`v'_(c) = (\omega L)/(2)`

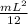
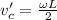
Thus

From these, potential energy about center of mass =
`(mL^(2)\omega'^(2))/(6)`

`mg(L)/(2) = (mL^(2)\omega'^(2))/(6)`

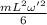
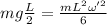
At the lowest point,
`\omega' = 7 rad/s`

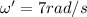
Thus

`mg(L)/(2) = (mL^(2)* 7^(2))/(6)`

`g = (49L)/(3)`

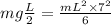
g = 9.8
`m/s^(2)`

`9.8 = (49L)/(3)`

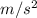
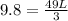
L = 0.6 m