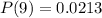Question

Arrivals at a fast-food restaurant follow a Poisson distribution with a mean arrival rate of 16 customers per hour. What is the probability that in the next hour there will be exactly 9 arrivals?

a. 0.7500

b. 0.1322

c. 0.0000

d. 0.0213

e. none of the above

Answer 1

d. 0.0213

Explanation:

If a variable follow a poisson distribution, the probability that x events happens in a specific time is given by:

`P(x)=(e^(-a)*a^(x) )/(x!)`

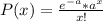
Where a is the mean number of events that happens in a specific time.

So, in this case, x is equal to 9 arrivals and a is equal to 16 customers per hour. Replacing this values, the probability is:

`P(9)=(e^(-16)*16^(9) )/(9!)`

`P(9)=0.0213`