Explanation:
Say
 is an element of
is an element of
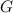 which might have more than 1 inverse. Let's call them
which might have more than 1 inverse. Let's call them
 , and
, and
 . So that
. So that
 has apparently two inverses,
has apparently two inverses,
 and
and
 .
.
This means that
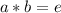 and that
and that
 (where
(where
 is the identity element of the group, and * is the operation of the group)
is the identity element of the group, and * is the operation of the group)
But so we could merge those two equations into a single one, getting
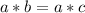
And operating both sides by b by the left, we'd get:
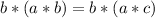
Now, remember the operation on any group is associative, meaning we can rearrange the parenthesis to our liking, gettting then:
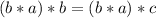
And since b is the inverse of a,
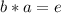 , and so:
, and so:
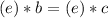
 (since e is the identity of the group)
(since e is the identity of the group)
So turns out that b and c, which we thought might be two different inverses of a, HAVE to be the same element. Therefore every element of a group has a unique inverse.