Question

A 594 Ω resistor, an uncharged 1.3 μF capacitor, and a 6.53 V emf are connected in series. What is the current in milliamps after one time constant? You are supposed to use a constant e can you please include what the value should be for this and all other constants.

Answer 1

6.88 mA

Step-by-step explanation:

Given:

Resistance, R = 594 Ω

Capacitance = 1.3 μF

emf, V = 6.53 V

Time, t = 1 time constant

Now,

The initial current, I₀ =
`\frac{\textup{V}}{\textup{R}}`

or

I₀ =
`\frac{\textup{6.53}}{\textup{594}}`

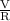
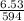
or

I₀ = 0.0109 A

also,

I =
`I_0[1-e^{-(t)/(\tau)}]`

here,

τ = time constant

e = 2.717

on substituting the respective values, we get

I =
`0.0109[1-e^{-(\tau)/(\tau)}]`

or

I =
`0.0109[1-2.717^(-1)]`

or

I = 0.00688 A

or

I = 6.88 mA