Answer:14.72 m/s
Step-by-step explanation:
Given
Initial velocity (u)=16.6 m/s
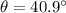
Horizontal velocity component (
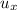 )=16.6cos40.9=12.54 m/s
)=16.6cos40.9=12.54 m/s
As the ball comes down so its vertical displacement is zero except 3 m elevation
Thus
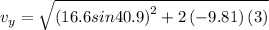
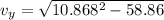
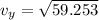
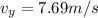
there will be no change is horizontal velocity as there is no acceleration
Therefore Final Velocity
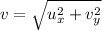
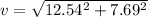
v=14.72 m/s