Answer:
Explanation:
We know that between 1 to 10 there are 5 even and 5 odd numbers.
We could get 4 even cards , 4 odd cards or 2 odd and 2 even cards
Let´s check all this combinations
Case 1: When all 4 numbers are even:
We are going to take 4 of the 5 even numbers in the box so we have

Case 2: When all 4 numbers are odd:
We are going to take 4 of the 5 odd numbers in the box, so we have

Case 3: When 2 are even and 2 are odd:
We are giong to take 2 from 5 even and odd cards in the box so we have

Remember that we obtain the probability from
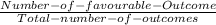
So we have the number of favourable outcomes but we need the Total cases for drawing four cards, so we have that:
We are taking 4 of the 10 cards:
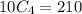
Hence we have that the probability that their sum is even
