Answer:
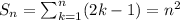
Explanation:
Let's take a look at the first few odd numbers and their sum.
Lets define
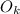 as the
as the
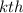 odd number as:
odd number as:
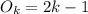
So we have:
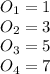
And lets define the sum of all the odd numbers from
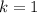 to
to
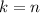 as:
as:
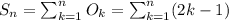
Lets now check some values of said sum:
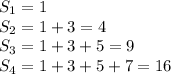
We can then observe than the sum up to
 equals
equals
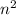
Let us then prove that this is the case by Induction.
First of all, we can prove this by an Induction Proof because we are taking all positive Integers. This is, we are working with the set of natural numbers
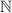 .
.
We want to prove that
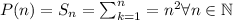
This is, we want to prove that the sum of all odd numbers from
 to
to
 equals
equals
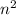 for all natural numbers.
for all natural numbers.
Now, in order to prove something by Induction we need to check 2 things:
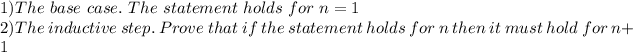
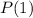 is immediate:
is immediate:
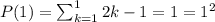
Now let's assume the statement holds for
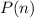 and let's take a look at
and let's take a look at
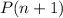
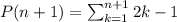
And we can rewrite it by taking the last term out as:
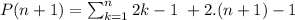
And by inductive hypothesis we know that
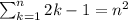
and then:
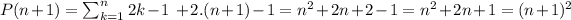
And we have the proof we were looking for!