Question

A cannon ball is fired with an arching trajectory such that at the highest point of the trajectory the cannon ball is traveling at 98 m/s. If the acceleration of gravity is 9.81 m/s^2, what is the radius of curvature of the cannon balls path at this instant?

Answer 1

The radius of curvature is 979 meter

Step-by-step explanation:

We have given velocity of the canon ball v = 98 m/sec

Acceleration due to gravity
`g=9.81m/sec^2`

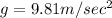
We know that at highest point of trajectory angular acceleration is equal to acceleration due to gravity

Acceleration due to gravity is given by
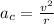`a_c=(v^2)/(r)`, here v is velocity and r is radius of curvature

So
`(98^2)/(r)=9.81`

r = 979 meter

So the radius of curvature is 979 meter