Question

Use a proof by contradiction to prove that the sum of two odd integers is even CM

Answer 1

The sum of two odd integers is even

Explanation:

Proof by contradiction:

We are going to assume that the sum of two odd integers is odd.

An odd integer is written as 2p+1 where p is an integer and an even integer is written as 2p where p is an integer

So, if the sum of two odd integers is odd we would have

`(2k+1) + (2p+1) = 2r+1\\2k+1+2p+1=2r+1\\2k+2p+2=2r+1\\2(k+p+1)=2r+1`

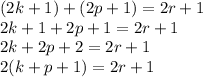
The left side of the equation is clearly an even number while the right side of the equation is odd. Therefore, our hypothesis is wrong and we can conclude that the sum of two odd integers is even.