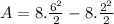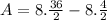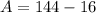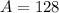Question

If f(x)=8x then what is the area enclosed by the graph of the function, the horizontal axis, and vertical lines at x=2 and x=6

Answer 1

`A=128`

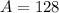
Explanation:

First of all we need to graph f(x)=8x, (First picture)

Now we have to calculate the area enclosed by the graph of the function, the horizontal axis, and vertical lines at
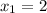`x_(1)=2` and
`x_(2)=6` ,

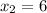The area that we have to calculate is in pink (second picture).

The function is positive and the domain is
`[2,6]` then we can calculate the area with this formula:

`A=\int\limits^b_a {f(x)} \, dx`,

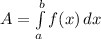In this case
`b=x_(2) , a=x_(1)`

`A=\int\limits^6_2 {8x} \, dx = 8\int\limits^6_2 {x} \, dx`

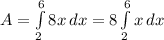
The result of the integral is,

`A=8(x^(2))/(2)`, but the integral is defined in [2,6] so we have to apply Barrow's rule,

Barrow's rule:

If f is continuous in [a,b] and F is a primitive of f in [a,b], then:

`\int\limits^b_a {f(x)} \, dx =F(b)-F(a)`

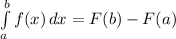
Applying Barrow's rule the result is:

`A=8.(6^(2) )/(2)-8.(2^(2) )/(2)`

`A=8.(36)/(2) -8.(4)/(2)`

`A=144-16`

`A=128`