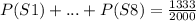Question

Suppose that coin 1 hasprobability 0.7 of coming up

heads, and coin 2 has probability 0.6of coming up heads. If the
coin flipped today comes up heads, thenwe select coin 1 to flip
tomorrow, and if it comes up tails, thenwe select coin 2 to flip
tomorrow. If the coin initially flipped isequally likely to be coin
1 or coin 2, then what is the probabilitythat the coin flipped on
the 3rd day after the initial flip is coin1?

Answer 1

`(1333)/(2000)`

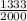
Explanation:

We want to compute the probabily of being flipping coin1 in the third day. Observe that in day zero (the day were the coin to be flipped is chosen randomly with equal probability to be coin1 or coin2), day 1 and day 2 we will flip coin1 or coin2. So, there are 8 possible scenarios to consider:

`S1=(1,1,1,1)\\S2=(1,1,2,1)\\S3=(1,2,1,1)\\S4=(1,2,2,1)\\S5=(2,1,1,1)\\S6=(2,1,2,1)\\S7=(2,2,1,1)\\S8=(2,2,2,1)`

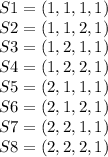
Where S1 is the scenario where we flip coin1 everyday. S2 is the scenario where we flip coin1 the day zero and first day, coin2 the second day, and again coin1 the third day. S3,...,S8 are defined the same.

Observe that the probability to flip coin1 the third day is equal to the sum of
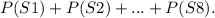`P(S1)+P(S2)+...+P(S8).` To compute this probabilities we will define:

`P(1,1)=`Probability to flip coin1 one day given that coin1 was flipped the day before.

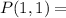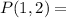`P(1,2)=`Probability to flip coin2 one day given that coin1 was flipped the day before.

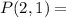`P(2,1)=`Probability to flip coin1 one day given that coin2 was flipped the day before.

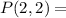`P(2,2)=`Probability to flip coin2 one day given that coin2 was flipped the day before.

Then, using the question information, we can conclude that

`P(1,1)=0.7, P(1,2)=0.3, P(2,1)=0.6, P(2,2)=0.4`

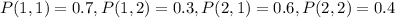
With this we can compute P(S1),...,P(S8) as follows:

`P(S1)=(1)/(2)P(1,1)*P(1,1)*P(1,1)=(1)/(2)*((7)/(10))^3=(343)/(2000)\\\\P(S2)=(1)/(2)P(1,1)*P(1,2)*P(2,1)=(1)/(2)*(7)/(10)*(3)/(10)*(6)/(10)=(126)/(2000)\\\\P(S3)=(1)/(2)P(1,2)*P(2,1)*P(1,1)=(1)/(2)*(3)/(10)*(6)/(10)*(7)/(10)=(126)/(2000)\\\\P(S4)=(1)/(2)P(1,2)*P(2,2)*P(2,1)=(1)/(2)*(3)/(10)*(4)/(10)*(6)/(10)=(72)/(2000)\\\\`

`P(S5)=(1)/(2)P(2,1)*P(1,1)*P(1,1)=(1)/(2)*(6)/(10)*(7)/(10)*(7)/(10)=(294)/(2000)\\\\P(S6)=(1)/(2)P(2,1)*P(1,2)*P(2,1)=(1)/(2)*(6)/(10)*(3)/(10)*(6)/(10)=(108)/(2000)\\\\P(S7)=(1)/(2)P(2,2)*P(2,1)*P(1,1)=(1)/(2)*(4)/(10)*(6)/(10)*(7)/(10)=(168)/(2000)\\\\P(S8)=(1)/(2)P(2,2)*P(2,2)*P(2,1)=(1)/(2)*(4)/(10)*(4)/(10)*(6)/(10)=(96)/(2000)\\\\`

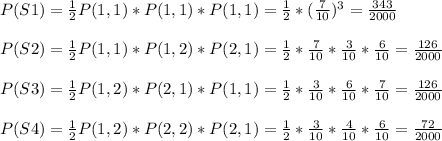
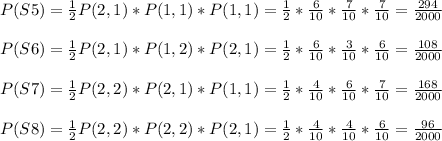
Finally, the probability to flip coin1 the third day is

`P(S1)+...+P(S8)=(1333)/(2000)`