Question

Use a direct proof to show that the product of two odd integers is odd.

Answer 1

Explanation:

The proof by the direct method that the product of two odd numbers is odd integer number, is the following:

Let
`z_1` and
`z_2` be two odd integers, then
`z_1 = 2a+1` and
`z_2 = 2b +1`, for some integers a and b.

`z_1z_2 = (2a + 1) (2b + 1)\\\\z_1z_2 = 4ab + 2a + 2b + 1\\\\z_1z_2 = 2 (2ab + a + b) +1\\\\z_1z_2 = 2n + 1`

where
`n = 2ab + a + b`, which guarantees that
`n` is an integer number. In this way,
`z_1z_2` is an odd integer.

Answer 2

Explanation:

A direct proof is a method that takes an statement p, which we assume to be true, and use it to show directly that another statement q is true. So this method has the following steps:

1. Assume the statement p is true
2. Use what we know about p and other facts as necessary to deduce that another statement q is true, that is show p ⇒ q is true.

Fact that we need to use:

Every odd integer can be written in the form 2m + 1 for some unique other integer m

Let p be the statement a and b be odd integers and q be the statement that the product of a and b is odd.

Proposition if a and b are odd, then the product of a and b is odd

Proof: Assume that a and b are odd integers, the by definition a = 2m + 1 and b = 2n + 1 for some integers m and n. we will now use this to show that the product of a and b is odd.

`a\cdot b= (2m+1) \cdot (2n+1)\\a\cdot b = 2m\cdot 2n+2m+2n+1\\a\cdot b =4mn+2m+2n+1\\a\cdot b = 2(2mn+2m+2n) +1\\\:If  \:k=2mn+2m+2n\\a\cdot b = 2k+1`

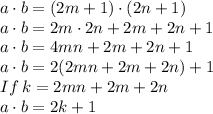
Hence we have shown that the product of a and b is odd since 2k + 1 is and odd integer. Therefore we have shown that p ⇒ q and so we have completed our proof.