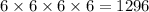Answer:
a) 6561
b) 3024
c) 1296
Explanation:
Given : Using the digits 1 through 9.
To find : The number of different 4-digit numbers such that :
(a) Digits can be used more than once.
(b) Digits cannot be repeated. 2 .
(c) Digits cannot be repeated and must be written in increasing order.
Solution :
Digits are 1,2,3,4,5,6,7,8,9
We have to form different 4-digit number let it be _ _ _ _
(a) Digits can be used more than once.
For first place there are 9 possibilities.
For second place there are 9 possibility as number repeats.
Same for third and fourth we have 9 possibility.
The number of ways are
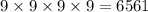
(b) Digits cannot be repeated.
For first place there are 9 possibilities.
For second place there are 8 possibility as number do not repeats.
For third place there are 7 possibility as number do not repeats.
For fourth place there are 6 possibility as number do not repeats.
The number of ways are

c) Digits cannot be repeated and must be written in increasing order.
The number which we can use on first position are 1,2,3,4,5,6 i.e. 6
The number which we can use on second position are 2,3,4,5,6,7 i.e. 6
The number which we can use on third position are 3,4,5,6,7,8 i.e. 6
The number which we can use on fourth position are 4,5,6,7,8,9 i.e. 6
Total number of ways are