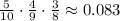Question

An urn contains ten marbles, of which give are green, two

areblue, and three are red. Three marbles are to be drawn from
theurn, one at a time without replacement. What is the
probabilitythat all three marbles drawn will be green?

Answer 1

`(5\cdot 4\cdot 3)/(10\cdot 9 \cdot 8)\approx 0.083`

Explanation:

Getting all three marbles of green color only happens if every draw is a green marble. On the first marble draw, the urn has 10 marbles in it, out of which 5 are green. So the probability of drawing a green marble on this first draw is
`(5)/(10)`

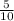
Then, once this has happened, the second draw also needs to be a green marble. At this point in the urn there are only 9 marbles left, and only 4 of them are green. So the probability of drawing a green marble at this point is
`(4)/(9)`

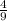
Afterwards, on the last draw, a green marble also needs to be drawn. At this point there are only 8 marbles left on the urn, and only 3 of them are green. So the probability of drawing a green marble on this last draw is
`(3)/(8)`

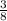
Therefore the probability of drawing all three marbles of green color is

`(5)/(10)\cdot(4)/(9)\cdot(3)/(8)\approx 0.083`