Question

In how many ways can 3 girls divide 10 pennies if each must end up with at least one penny?

Answer 1

36.

Step-by-step explanation:

We are asked to find the number of ways in which 3 girls can divide 10 pennies such that each must end up with at least one penny.

The selection can be done by selecting two dividing likes between the 10 pennies such that the set is divided into three parts.

Since each girl must have one penny, so no girl can have 0 penny. So the dividing like cannot be placed at end points, beginning and at the end. Therefore, we are left with 9 positions.

Now we need to find number of ways to select two positions out of the 9 positions that is C(9,2).

`_(2)^(9)\textrm{C}=(9!)/(7!*2!)=(9*8*7!)/(7!*2*1)=(9*8)/(2)=9*4=36`

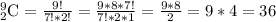
Therefore, there are 36 ways to divide 10 pennies between 3 girls.