Question

A stone is tied to a string and whirled around in a circle at

aconstant speed. Is the string more likely to break when the
circleis horizontal or when it is vertical? Account for your
answer,assuming the constant speed is the same in each case.

Answer 1

Vertical circle.

Step-by-step explanation:

According to the question:

When the stone tied string moves in horizontal circle, then the tension in the string is provided by the centripetal force.

When the stone tied string moves in a vertical circle, then the tension is provided by the centripetal force as well as its weight.

Thus the probability of breaking in the vertical circle is more.

Refer to the fig shown:

In case of horizontal circle:

The centripetal force for a circle of radius R is given by:

`F_(c) = (mv_(P)^(2))/(R) = mg`

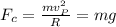
Now, at point P:

`mg - T = (mv_(P)^(2))/(R)`

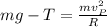
Since, T = 0

`mg - 0 = (mv_(P)^(2))/(R)`

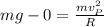
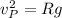`v_(P)^(2) = Rg` (1)

Now, at point Q:

`T - mg = (mv_(Q)^(2))/(R)` (2)

Also, by using the law of conservation of energy, total mechanical energy at point P and Q will be conserved:

`(1)/(2)mv_(P)^(2) + mg(2R) = (1)/(2)mv_(Q)^(2) + mg(0)`

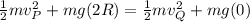
Using eqn (1):

`(1)/(2)gR + 2gR = (1)/(2)v_(Q)^(2)`

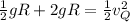
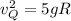`v_(Q)^(2) = 5gR` (3)

Now, using eqn (2) and (3):

`T  = (m5gR)/(R) + mg = 6mg`

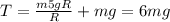
Thus tension at point Q is greater than the force at point P.