Question

A survey of 510 adults aged 18-24 year olds was conducted in which they were asked what they did last Friday night. It found: 161 watched TV 196 hung out with friends 161 ate pizza 28 watched TV and ate pizza, but did not hang out with friends 29 watched TV and hung out with friends, but did not eat pizza 47 hung out with friends and ate pizza, but did not watch TV 43 watched TV, hung out with friends, and ate pizza How may 18-24 year olds did not do any of these three activities last Friday night?

Answer 1

To find the number of 18-24 year olds who did not do any of the three activities last Friday night, we can use the principle of inclusion-exclusion. By subtracting the number of people who did at least one of the activities from the total number of participants, we find that 455 individuals did not participate in watching TV, hanging out with friends, or eating pizza.

Step-by-step explanation:

To find the number of 18-24 year olds who did not do any of the three activities (watch TV, hang out with friends, eat pizza), we need to subtract the number of people who did at least one of these activities from the total number of participants. We can use the principle of inclusion-exclusion to solve this problem.

Let's define:

• A = number of people who watched TV
• B = number of people who hung out with friends
• C = number of people who ate pizza

From the given information, we know:

• A = 161
• B = 196
• C = 161
• A ∩ C' (watched TV and ate pizza, but did not hang out with friends) = 28
• A ∩ B' (watched TV and hung out with friends, but did not eat pizza) = 29
• B ∩ C' (hung out with friends and ate pizza, but did not watch TV) = 47
• A ∩ B ∩ C (watched TV, hung out with friends, and ate pizza) = 43

To find the number of people who did not do any of these activities, we can use the formula:

n(A' ∩ B' ∩ C') = n(U) - n(A) - n(B) - n(C) + n(A ∩ B) + n(A ∩ C) + n(B ∩ C) - n(A ∩ B ∩ C)

Substituting the known values, we have:

n(A' ∩ B' ∩ C') = 510 - 161 - 196 - 161 + 28 + 29 + 47 - 43

n(A' ∩ B' ∩ C') = 455

Therefore, there were 455 18-24 year olds who did not do any of the three activities last Friday night.

Answer 2

182 of these adults did not do any of these three activities last Friday night.

Step-by-step explanation:

To solve this problem, we must build the Venn's Diagram of this set.

I am going to say that:

-The set A represents the adults that watched TV

-The set B represents the adults that hung out with friends.

-The set C represents the adults that ate pizza

-The set D represents the adults that did not do any of these three activities.

We have that:

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

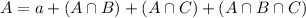
In which a is the number of adults that only watched TV,
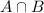`A \cap B` is the number of adults that both watched TV and hung out with friends,
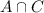`A \cap C` is the number of adults that both watched TV and ate pizza, is the number of adults that both hung out with friends and ate pizza, and
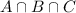`A \cap B \cap C` is the number of adults that did all these three activies.

By the same logic, we have:

`B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

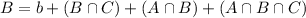
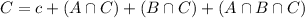
This diagram has the following subsets:

`a,b,c,D,(A \cap B), (A \cap C), (B \cap C), (A \cap B \cap C)`

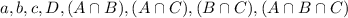
There were 510 adults suveyed. This means that:

`a + b + c + D + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 510`

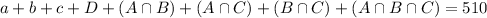
We start finding the values from the intersection of three sets.

Solution:

43 watched TV, hung out with friends, and ate pizza:

`A \cap B \cap C = 43`

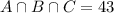
47 hung out with friends and ate pizza, but did not watch TV:

`B \cap C = 47`

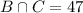
29 watched TV and hung out with friends, but did not eat pizza:

`A \cap B = 29`

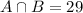
28 watched TV and ate pizza, but did not hang out with friends:

`A \cap C = 28`

161 ate pizza

`C = 161`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

`161 = c + 28 + 47 + 43`

`c = 43`

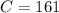
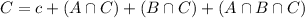
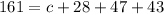
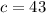
196 hung out with friends

`B = 196`

`196 = b + 47 + 29 + 43`

`b = 77`

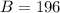
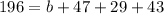
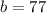
161 watched TV

`A = 161`

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

`161 = a + 29 + 28 + 43`

`a = 61`

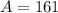
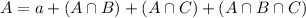
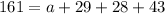
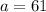
How may 18-24 year olds did not do any of these three activities last Friday night?

We can find the value of D from the following equation:

`a + b + c + D + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 510`

`61 + 77 + 43 + D + 29 + 28 + 47 + 43 = 510`

`D = 510 - 328`

`D = 182`

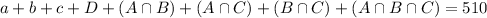
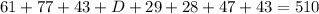
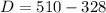
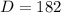
182 of these adults did not do any of these three activities last Friday night.