Answer:
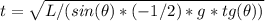
Step-by-step explanation:
The mass will have a weight, and since it is on a surface it will have a normal reaction.
The vertical component of the normal reaction will be equal and opposite to the weight.
w = g * m
Nv = N * sin(θ)
N is the normal reaction and Nh its vertical component
Nv = -w
N * sin(θ) = -g * m
The horizontal component of the normal will be
Nh = N * cos(θ)
N = Nh / cos(θ)
Then:
Nh / cos(θ) * sin(θ) = -g * m
sin/cos = tg
Nh * tg(θ) = -g * m
The horizontal component of the normal force will be the only force in the horizontal direction
It will cause an acceleration
Nh = ah * m
Then
ah * m * tg(θ) = -g * m
Simplifying the mass on each side
ah * tg(θ) = -g
ah = -g * tg(θ)
The mass will slide from a height related to the lenght of the ramp
L = D * sin(θ)
D = L / sin(θ) This is the distance it will slide
We set up a reference system with origin at the top of the ramp and the positive X axis pointing down the ramp in the direction of the slope.
In this reference system:
X(t) = X0 + V0*t + 1/2 * a * t^2
X0 = 0
V0 = 0
Then
X(t) = -1/2 * g * tg(θ) * t^2
It will move the distance D
L / sin(θ) = -1/2 * g * tg(θ) * t^2
t^2 = L / ( sin(θ) * (-1/2) * g * tg(θ) )
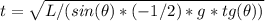
The negative sign will dissapear because gravity has a negative sign too.