A bacteria culture starts with 200 bacteria and grows at a rate proportional to its size. After 6 hours there will be 1200 bacteria (1) Express the population after I hours as a…

Question

asked Jan 28, 2020 82.8k views

1 Answer

Cyroxis · Answer 1 · 2020-02-04T08:13:31+0000

Answer:

We are given that the rate of change is proportional to its size S

So,
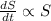
$(dS)/(dt) \propto S$

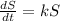
(dS)/(dt) = kS

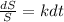
(dS)/(S) = kdt

Integrating both sides

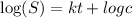
$\log(S)= kt + log c$

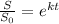
(S)/(S_0)=e^(kt)

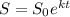
S=S_0 e^(kt)

S is the population after t hours

S_0 is the initial population

Now we are given that After 6 hours there will be 1200 bacteria

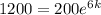
1200=200 e^(6k)

6=e^(6k)

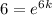
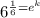
$6^{(1)/(6)=e^(k)$

So,
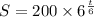
$S=200 * 6^{(t)/(6)$

a)Now the population after t hours as a function of t;
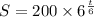
$S=200 * 6^{(t)/(6)$

b) What will be the population after 7 hours?

Substitute t = 7 hours

A bacteria culture starts with 200 bacteria

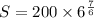
$S=200 * 6^{(7)/(6)}$

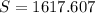
c) How long will it take for the population to reach 1750 ?

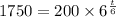
$1750=200 * 6^{(t)/(6)$

$(1750)/(200) =6^{(t)/(6)$

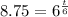
$8.75 =6^{(t)/(6)$

t=7.26

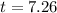
So, it will take 7.2 hours for the population to reach 1750