Question

Find the period and amplitude of the function. y-2sin 6x Give the exact values, not decimal approximations. Period: 2 Amplitude:

Answer 1

Amplitude=2

Period=
`(\pi)/(3)`

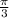
Explanation:

We are given that
`y=2sin6x`

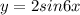
We have to find the value of period and amplitude of the given function

We know that
`y=a sin(bx+c)+d`

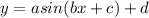
Where a= Amplitude of function

Period of sin function =
`(2\pi)/(\mid b \mid)`

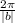
Comparing with the given function

Amplitude=2

Period=
`(2\pi)/(6)=(\pi)/(3)`

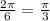
Hence, period of given function=
`(\pi)/(3)`

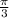
Amplitude=2