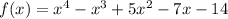Answer:
a.
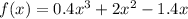
b.
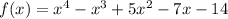
Explanation:
A polynomial of degree three satisfies the four points offered, in this way, if we evaluate said polynomial in the points, we can generate a linear system of four equations with four incognites that when solved will allow us to know the coefficients.
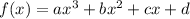
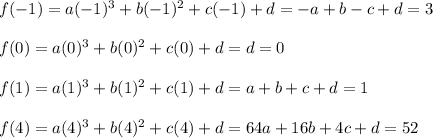
The linear system is:
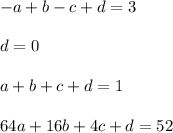
The solution of the linear system is:
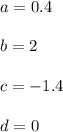
Then the function is:
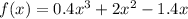
b. A polynomial of degree four satisfies the five points offered, in this way, if we evaluate said polynomial in the points, we can generate a linear system of five equations with five incognites that when solved will allow us to know the coefficients.
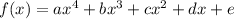
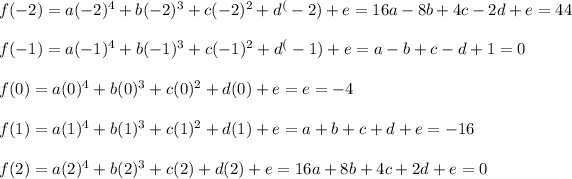
The linear system is:
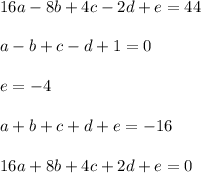
The solution of the linear system is:

Then the function is: