To prove that V is a vector space we must prove that the sum define on it satisfy conmutativiy, asociativity and existence of the neutral element and inverses. Also, the scalar multiplication define on V must satisfy distributivity propertie with respect to the sum and viceversa, and an asosiativity too in the sense that
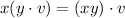 for
for
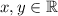 and
and
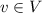 . One can prove with this that the neutral element for the sum is unique. But with your operations you have two neutral elements for
. One can prove with this that the neutral element for the sum is unique. But with your operations you have two neutral elements for
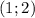

and
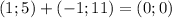
So, you dont have a vector space.