Answer:
The 105th term of given sequence is
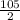 .
.
Explanation:
The given sequence is
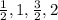
It can be rewritten as

Here the first term is 0.5.
It is an arithmetic sequence because it has common difference.

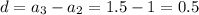
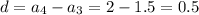
The nth term of an AP is
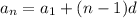
where,
 is first term and d is common difference.
is first term and d is common difference.
Substitute
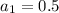 and
and
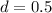 in the above formula.
in the above formula.
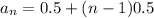
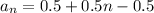

We need to find the 105th term of given sequence.
Substitute n=105 in the above equation.
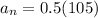
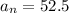
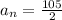
Therefore the 105th term of given sequence is
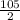 .
.