Question

The engine is mounted on a foundation block which is spring - supported. Describe the steady - state vibration of the system if the block and engine have a total weight of 7500 N ( 750 kg) and the engine, when running, creates an impressed force F = (250 sin 2/) N, where t is in seconds. Assume that the system vibrates only in the vertical direction, with the positive displacement measured downward, and that the total stiffness of the springs can be represented as k = 30 kN/m. Determine the rotational speed omega of the engine which will cause resonance.

Answer 1

wr = 6.32 rad/s

Step-by-step explanation:

m = 750 kg

k = 30 kN/m

This system has no dampening, therefore the resonance frequency will simply be the natural frequency of the system.

`wr = w0 = \sqrt{(k)/(m)}`

`wr = \sqrt{(30000)/(750)} = 6.32 rad/s`

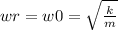
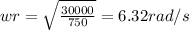
In this case the force applied doesn't matter. because we are calculating the resonance frequency.