A survey of 1,168 tourists visiting Orlando was taken. Of those surveyed: 266 tourists had visited LEGOLAND 295 tourists had visited Universal Studios 87 tourists had visited both the Magic Kingdom and - QAmmunity.org

A survey of 1,168 tourists visiting Orlando was taken. Of those surveyed: 266 tourists had visited LEGOLAND 295 tourists had visited Universal Studios 87 tourists had visited both the Magic Kingdom and

asked Jul 17, 2020 190k views

1 Answer

Answer:

624 tourists only visited the Magic Kindgom.

Explanation:

To solve this problem, we must build the Venn's Diagram of this set.

I am going to say that:

-The set A represents the tourists that visited LEGOLAND

-The set B represents the tourists that visited Universal Studios

-The set C represents the tourists that visited Magic Kingdown.

-The value d is the number of tourists that did not visit any of these parks, so:
d = 74

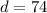
We have that:

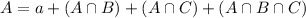
$A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)$

In which a is the number of tourists that only visited LEGOLAND,
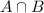$A \cap B$ is the number of tourists that visited both LEGOLAND and Universal Studies,
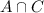$A \cap C$ is the number of tourists that visited both LEGOLAND and the Magic Kingdom. and
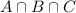$A \cap B \cap C$ is the number of students that visited all these parks.

By the same logic, we have:

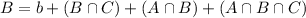
$B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)$

$C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)$

This diagram has the following subsets:

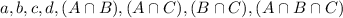
$a,b,c,d,(A \cap B), (A \cap C), (B \cap C), (A \cap B \cap C)$

There were 1,168 tourists suveyed. This means that:

$a + b + c + d + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 1,168$

We start finding the values from the intersection of three sets.

The problem states that:

16 tourists had visited all three theme parks. So:

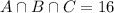
$A \cap B \cap C = 16$

91 tourists had visited both LEGOLAND and Universal Studios. So:

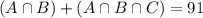
$(A \cap B) + (A \cap B \cap C) = 91$

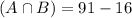
$(A \cap B) = 91-16$

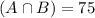
$(A \cap B) = 75$

68 tourists had visited both the Magic Kingdom and Universal Studios. So

$(B \cap C) + (A \cap B \cap C) = 68$

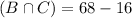
$(B \cap C) = 68-16$

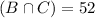
$(B \cap C) = 52$

87 tourists had visited both the Magic Kingdom and LEGOLAND

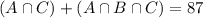
$(A \cap C) + (A \cap B \cap C) = 87$

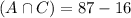
$(A \cap C) = 87-16$

$(A \cap C) = 71$

295 tourists had visited Universal Studios

B = 295

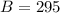
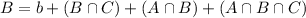
$B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)$

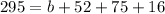
295 = b + 52 + 75 + 16

b + 143 = 295

b = 152

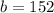
266 tourists had visited LEGOLAND

A = 266

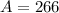
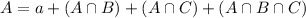
$A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)$

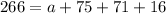
266 = a + 75 + 71 + 16

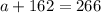
a + 162 = 266

a = 104

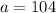
How many tourists only visited the Magic Kingdom (of these three)?

This is the value of c, the we can find in the following equation:

$a + b + c + d + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 1,168$

104 + 152 + c + 74 + 75 + 71 + 52 + 16 = 1,168

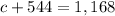
c + 544 = 1,168

c = 624

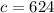
624 tourists only visited the Magic Kindgom.

Guferos answered Jul 24, 2020

5.4k points

Search QAmmunity.org