Question

In an arithmetic​ sequence, the nth term an is given by the formula An=a1+(n−1)d​, where a1is the first term and d is the common difference.​ Similarly, in a geometric​ sequence, the nth term is given by an=a1•rn−1.

Use these formulas to determine the indicated term in the given sequence.

The 19th term of 19​,42​,65​,88​,...

Answer 1

Answer: 433

Explanation:

The given sequence : 19​,42​,65​,88​,...

Here we can see that the difference in each of the two consecutive terms is 23. [88-65=23, 65-42=23, 42-19=23]

i.e. it has a common difference of 23.

Therefore, it is an arithmetic sequence .

In an arithmetic​ sequence, the nth term an is given by the formula
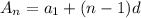`A_n=a_1+(n-1)d` , where
`a_1` is the first term and d is the common difference.​

For the given sequence ,
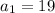`a_1=19` and
`d=23`

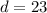
Then, to find the 19th term of the sequence, we put n= 19 in the above formula:-

`A_(19)=19+(19-1)(23)=19+(18)(23)=19+414+433`

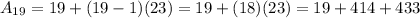
Hence, the 19th term of the sequence = 433