Question

For the following​ sequence, determine if it is an arithmetic​sequence, a geometric​ sequence, or neither. If it is either arithmetic or​ geometric, give the next term in the sequence.

5​, 8​,13​, 21​, 34​, 55,...

Answer 1

Neither

Explanation:

We are given that a sequence

5,8,13,21,34,55,....

We have to determine the sequence is an arithmetic , geometric or neither.

`a_1=5,a_2=8,a_3=13,...a_6=55`

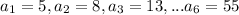
We know that if a sequence is an arithmetic then the difference between consecutive terms are equal.

If a sequence is geometric then the ratio of consecutive terms is constant.

`d_1=a_2-a_1=8-5=3`

`d_2=a_3-a_2=13-8=5`

`d_1\\eq d_2`

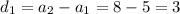
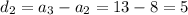
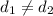
Hence, the difference between the consecutive terms is not equal .Therefore, sequence is not an arithmetic sequence.

`r_1=(a_2)/(a_1)=(8)/(5)`

`r_2=(a_3)/(a_2)=(13)/(8)`

`r_1\\eq r_2`

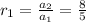
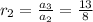
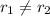
Hence, the ratio of consecutive terms is not equal .Therefore, given sequence is not geometric sequence.

Therefore, given sequence is not an arithmetic nor geometric sequence.