Answer:
88
Explanation:
We are given that in arithmetic sequence , the nth term
 is given by the formula
is given by the formula
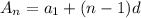
Where
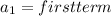
d=Common difference
In an geometric sequence, the nth term is given by
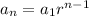
Where r= Common ratio
1,4,7,10,..
We have to find 30th term.
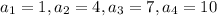
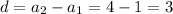
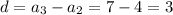
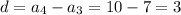



Therefore, given sequence is an arithmetic sequence because the difference between consecutive terms is constant.
Substitute n=30 , d=3 a=1 in the given formula of arithmetic sequence
Then, we get
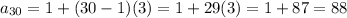
Hence, the 30th term of sequence is 88.