Question

An object is supported by a crane through a steel cable of 0.02m diameter. If the natural swinging of the equivalent pendulum is 0.95 rad/s and the natural time period of the axial vibration is found to be 0.35 sec. What is the mass of the object.

Answer 1

22.90 × 10⁸ kg

Step-by-step explanation:

Given:

Diameter, d = 0.02 m

ωₙ = 0.95 rad/sec

Time period, T = 0.35 sec

Now, we know

T=
`2\pi\sqrt{(L)/(g)}`

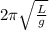
where, L is the length of the steel cable

g is the acceleration due to gravity

0.35=
`2\pi\sqrt{(L)/(9.81)}`

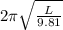
or

L = 0.0304 m

Now,

The stiffness, K is given as:

K =
`\frac{\textup{AE}}{\textup{L}}`

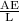
Where, A is the area

E is the elastic modulus of the steel = 2 × 10¹¹ N/m²

or

K =
`((\pi)/(4)d^2*2*10^11)/(0.0304)`

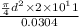
or

K = 20.66 × 10⁸ N

Also,

Natural frequency, ωₙ =
`\sqrt{(K)/(m)}`

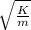
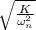
or

mass, m =
`\sqrt{(K)/(\omega_n^2)}`

or

mass, m =
`\sqrt{(20.66*10^8)/(0.95^2)}`

mass, m = 22.90 × 10⁸ kg