Answer:
1.No, because inverse does not exist.
2.No, because inverse does not exist.
Explanation:
We are given that X be a set and let P(X) be the power set of X.
a. We have to tell P(X) with binary operation
A*B=
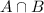 form a group.
form a group.
Suppose, x={1,2}
P(X)={
 ,{1},{2},{1,2}}
,{1},{2},{1,2}}
1.Closure property:
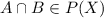
{1}
 {2}=
{2}=
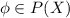
It is satisfied for all
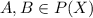
2.Associative property:
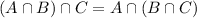
If A={1},B={2},C={1,2}
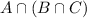 ={1}
={1}
 ({2}
({2}
 {1,2})={1}
{1,2})={1}
 {2}=
{2}=

 =({1}
=({1}
 {2})
{2})
 {1,2}=
{1,2}=
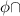 {1,2}=
{1,2}=

Hence, P(X) satisfied the associative property.
3.Identity :
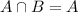 Where B is identity element of P(X)
Where B is identity element of P(X)
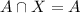
It is satisfied for every element A in P(X).
Hence, X is identity element in P(X)
4.Inverse :
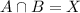 Where B is an inverse element of A in P(x)
Where B is an inverse element of A in P(x)
It can not be possible for every element that satisfied
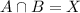
Hence, inverse does not exist.
Therefore, P(X) is not a group w.r.t to given binary operation.
2.We have to tell P(X) with the binary operation
A*B=
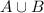 form a group
form a group
Similarly,
For set X={1,2}
P(X)={
 ,{1},{2},{1,2}}
,{1},{2},{1,2}}
1.Closure property:If A and B are belongs to P(X) then
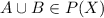 for all A and B belongs to P(X).
for all A and B belongs to P(X).
2.Associative property:
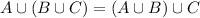
If A={1},B={2},C{1,2}
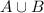 ={1}
={1}
 {2}={1,2}
{2}={1,2}
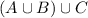 ={1,2}
={1,2}
 {1,2}={1,2}
{1,2}={1,2}
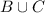 ={2}
={2}
 {1,2}={1,2}
{1,2}={1,2}
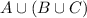 ={1}
={1}
 {1,2}={1,2}
{1,2}={1,2}
Hence, P(X) satisfied the associative property.
3.Identity :
 Where B is identity element of P(X)
Where B is identity element of P(X)
Only
 is that element for every A in P(X) that satisfied
is that element for every A in P(X) that satisfied

Hence,
 is identity element of P(X) w.r.t union.
is identity element of P(X) w.r.t union.
4.Inverse element :
 where B is an inverse element of A in P(X)
where B is an inverse element of A in P(X)
It is not possible for every element that satisfied the property.
Hence, inverse does not exist for each element in P(X).
Therefore, P(X) is not a group w.r.t binary operation.