Answer with explanation:
Given : Significance level :
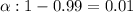
Critical value :
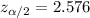
Margin of error :
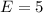
Standard deviation :
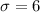
The formula to find the sample size :-
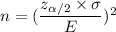
Then, the sample size will be :-
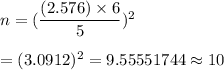
The minimum final size sample required is 10.
If only 30 percent of households have a cat, then the proportion of households have a cat = 0.3
The formula to find the sample size :-
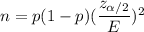
Then, the sample size will be :-
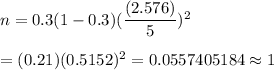
Hence, the initial number of households that need to be contacted =1