Answer:
43.3 m
Step-by-step explanation:
d1 = 25.1 m in 15.4° west of north
d2 = 38.8 m in 23.1° south of west
Write the displacements in vector form

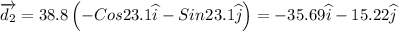
The resultant displacement is given by


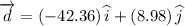
The magnitude of the resultant displacement is given by
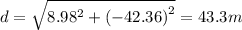
Thus, you are 43.3 m far from your starting point.