Question

A test charge of +4 µC is placed halfway between a charge of +6 µC and another of +2 µC separated by 20 cm. (a) What is the magnitude of the force (in N) on the test charge?

(b) What is the direction of this force (away from or toward the +6 µC charge)?
a. away from the +6 µC charge or
b. toward the +6 µC charge

Answer 1

(a) Magnitude: 14.4 N

(b) Away from the +6 µC charge

Step-by-step explanation:

As the test charge has the same sign, the force that the other charges exert on it will be a repulsive force. The magnitude of each of the forces will be:

`F_e = K(qq_(test))/(r^2)`

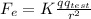
K is the Coulomb constant equal to 9*10^9 N*m^2/C^2, q and qtest is the charge of the particles, and r is the distance between the particles.

Let's say that a force that goes toward the +6 µC charge is positive, then:

`F_e_1 = K(q_1q_(test))/(r^2)=-9*10^9 (Nm^2)/(C^2) (6*10^(-6)C*4*10^(-6)C)/((0.1m)^2) =-21.6 N`

`F_e_2 = K(q_2q_(test))/(r^2)=9*10^9 (Nm^2)/(C^2) (2*10^(-6)C*4*10^(-6)C)/((0.1m)^2) =7.2 N`

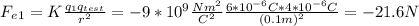
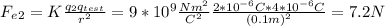
The magnitude will be:

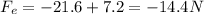`F_e = -21.6 + 7.2 = -14.4 N`, away from the +6 µC charge