Question

A hot air ballo0n is ascending straight up at a constant

speedof 7.0 m/s. When the balloon is 12.0 m above the ground, agun
fires a pellet straight up from ground level with an initialspped
of 30.0 m/s. Along the paths of the ballon and thepellet, there are
two places where each of them has the altitude atthe same time. How
far above ground level are theseplaces?

Answer 1

Answer: The two places altitudes are: 16.17 m and 40.67 m

Step-by-step explanation:

Hi!

Lets call z to the vertical direction (z= is ground) . Then the positions of the balloon and the pellet, using the values of the velocities we are given, are:

`z_b =\text{balloon position}\\z_p=\text{pellet position}\\z_b=(7(m)/(s))t\\z_p=30(m)/(s)(t-t_0)-(g)/(2)(t-t_0)^2\\g=9.8(m)/(s^2)`

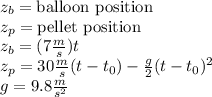
How do we know the value of t₀? This is the time when the pellet is fired. At this time the pellet position is zero: its initial position. To calculate it we know that the pellet is fired when the ballon is in z = 12m. Then:

`t_0=(12)/(7)s`

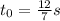
We need to know the when the z values of balloon and pellet is the same:

`z_b=z_p\\(7(m)/(s))t =30(m)/(s)(t-(12)/(7)s)-(g)/(2)(t-(12)/(7)s)^2`

We need to find the roots of the quadratic equation. They are:

`t_1=2.31s\\t_2=5.81`

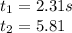
To know the altitude where the to objects meet, we replace the time values:

`z_1=16,17m\\z_2=40,67m`