Answer:
Distance from the net when she meets the return: 14,3 m
Step-by-step explanation:
First we need to know how much time it takes the ball to reach the net, the kinematycs general equation for position:
(1)
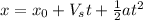
Taking the net as the origin (x = 0),
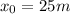 , velocity will be nagative
, velocity will be nagative
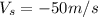 and assuming there is no friction wit air acceleration would be 0, so:
and assuming there is no friction wit air acceleration would be 0, so:
(2)
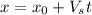
we want to know the time when it reaches the net so when x=0, replacing de values:
(3)
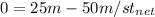
So:
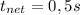
The opponent will return the ball at
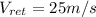 , the equation for the return of the ball will be:
, the equation for the return of the ball will be:
(4)
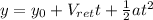
Note that here it start from the origin,
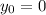 , as in the other case acceleration equals 0, and here we have to consider that the time starts when the ball reaches the net (
, as in the other case acceleration equals 0, and here we have to consider that the time starts when the ball reaches the net (
 ) so the time for this equiation will be
) so the time for this equiation will be
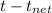 , this is only valid for
, this is only valid for
 :
:
(5)
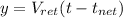
Coco starts running as soon as he serves so his equiation for position will be:
(6)

As in the first case it starts from 25m,
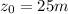 , acceleration equals 0 and velocity is negative
, acceleration equals 0 and velocity is negative
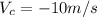 :
:
(7)
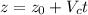
To get the time when they meet we have that
 , so from equiations (5) and (7):
, so from equiations (5) and (7):
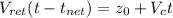
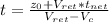
Replacing the values:
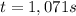
Replacing t in either (5) or (7):
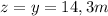
This is the distance to the net when she meets the return