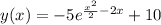Answer:
The solution for the initial value problem is:
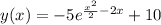
Explanation:
We have the following initial value problem:
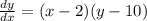
The first step is solving the differential equation. We can do this by the variable separation method. It means that every term with y in on one side of the equality, every term with x on the other side. So:
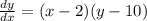
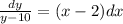
To find y in function of x, we integrate both sides.
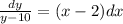

Solving each integral separately
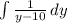
This one we solve by substitution
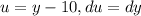
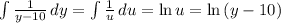
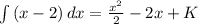
Now we have that:

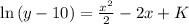
To solve for y, we apply the exponential to both sides, since the exponential and ln are inverse operations:
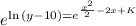

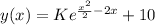
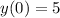 means that when
means that when
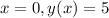 . So:
. So:
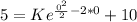
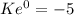
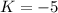
So, the solution for the initial value problem is: