Question

In a tensile test on a steel specimen, true strain is 0.171 at a stress of 263.8 MPa. When true stress is 346.2 MPa, true strain is 0.226. Determine strain hardening exponent, n, in the flow curve for the plastic region of this steel.

Answer 1

Answer:n=0.973

Step-by-step explanation:

Given

When True strain
`\left ( \epsilon _T_1\right )=0.171`

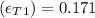
at
`\sigma _1=263.8 MPa`

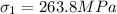
When True stress
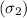`\left ( \sigma _2\right )`=346.2 MPa

true strain
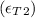`\left ( \epsilon _T_2\right )`=0.226

We know

`\sigma =k\epsilon ^n`

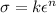
where
`\sigma`=True stress

`\epsilon`=true strain

n=strain hardening exponent

k=constant

Substituting value

`263.8=k\left ( 0.171\right )^n------1`

`346.2=k\left ( 0.226\right )^n-----2`

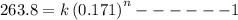
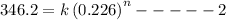
Divide 1 & 2 to get

`(346.2)/(263.8)=\left ( (0.226)/(0.171)\right )^n`

`1.312=\left ( 1.3216\right )^n`

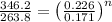
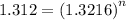
Taking Log both side

`ln\left ( 1.312\right )=nln\left ( 1.3216\right )`

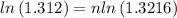
n=0.973