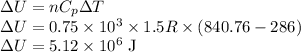Question

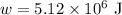
Calculate the work done in compressing adiabatically 3kg of helium (He) to one fifth of its original volume if it is initially at 13°C. Find the change in internal energy of the gas resulting from the compression. (cp/cv for monatomic gases is 1.667; gas constant for helium is 2079 K^-1 kg^-1)

Answer 1

Work done,
`w=5.12*10^(6)\ \rm J`

change in internal Energy ,
`\Delta U=5.12*10^6\ \rm J`

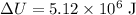
Step-by-step explanation:

Given:

• Mass of helium gas
  `m=3\ \rm kg`
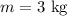
• initial temperature
  `T_i=286\ \rm K`

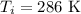
Since It is given that the process is adiabatic process it means that there is no exchange of heat between the system and surroundings

`T_iV_i^(\gamma -1)=T_fV_f^(\gamma -1)\\\\286* V_i^(\gamma -1)=T_f \left( (V_i)/(5) \right )^(\gamma -1)\\T_f=840.76\ \rm K`

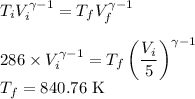
Let n be the number of moles of Helium given by

`n=(m)/(M)\\n=(3*10^3)/(4)\\n=0.75*10^3`

Work done in Adiabatic process

Let W be the work done

`W=(nR(T_1-T_2))/(\gamma-1)\\W=(0.75*10^3*8.314(286-840.76))/(1.67-1)\\W=-5.12* 10^6\ \rm J`

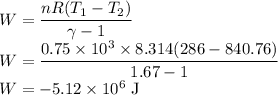
The Internal Energy change in any Process is given by

Let
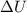`\Delta U` be the change in internal Energy

`\Delta U=nC_p\Delta T\\\Delta U=0.75*10^3*1.5R*(840.76-286)\\\Delta U=5.12*10^6\ \rm J`