Answer:
30.55 %
Step-by-step explanation:
Assumptions:
- l = initial length of the wire
- L = final length of the wire
- v = initial volume of the wire
- V = final volume of the wire
- a = initial cross sectional area of the wire
- A = final cross sectional area of the wire
- h = initial heat of generated by the wire
- H = final heat generated by the wire
- P = potential difference across the wire
- t = time for which the potential difference is created across the wire
- r = initial resistance of the wire
- R = final resistance of the wire
 = change in heat produced
= change in heat produced
According to the question, we have
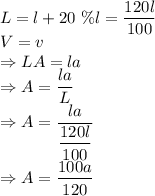
Using the formula of resistance of a wire in terms of its length, cross sectional area and the resistivity of the material, we have

Using the formula of heat generated by the wire for potential diofference created across its end for time t, we have

Hence, the percentage change in the heat produced in the wire is 30.55 %.