Answer:
The height of the cliff is 39.655 m
Given:
Height at which the arrow was shot, h = 1.3 m
Velocity of the arrow, u = 34 m/s
Angle,
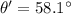
Time of the fight, t = 4.1 s
Solution:
Let the Height of the cliff be H
Since, the motion of the object is projectile motion and the direction of motion is vertical at some angle
Therefore, we consider the vertical component of velocity,
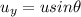 .
.
Now,
The Height of the cliff is given by applying the second equation of motion in the projectile:
Thus
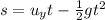
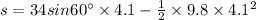
s = 38.355 m
Now, the height of the cliff, H:
H = s + h = 38.355 + 1.3 = 39.655 m