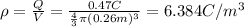Question

A ball of charge containing 0.47 C has radius 0.26 m. a) What is the electric field strength at a radius of 0.18 m?

b) What is E at 0.50 m?
c) What is E at infinity?
d) What is the volume charge density?

Answer 1

a) 4.325*10^10 V/m

b) 1.689*10^10 V/m

c) 0

d) 6.384 C/m^3

Step-by-step explanation:

Hello!

The electric field of a sphere of uniform charge is a piecewise function, let a be the raius of the sphere

For r<a:

`E = kQ(r)/(a^(3))`

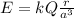
For r>a:

`E=kQ/r^(2)`

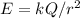
Since a=0.26m and k= 8.987×10⁹ N·m²/C²

a)

`E= 8.987*10^(9)(0.47C *0.18m)/((0.26m)^(3))`

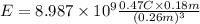
E=4.325*10^10 V/m

b)

`E= 8.987*10^(9)(0.47C)/((0.5m)^(2))`

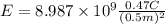
E=1.689*10^10 V/m

c)

Since r --> ∞ 1/r^2 --> 0

E(∞)=0

d)

The charge density may be obtained dividing the charge by the volume of the sphere:

`\rho = (Q)/(V) =(0.47C)/((4)/(3) \pi (0.26m)^(3))=6.384 C/m^(3)`