Question

Serving at a speed of 164 km/h, a tennis player hits the ball at a height of 2.23 m and an angle θ below the horizontal. The service line is 11.6 m from the net, which is 0.99 m high. What is the angle θ in degrees such that the ball just crosses the net? Give a positive value for the angle.

Answer 1

The angle θ is 6.1° below the horizontal.

Step-by-step explanation:

Please, see the figure for a description of the situation.

The vector "r" gives the position of the ball and can be expressed as the sum of the vectors rx + ry (see figure).

We know the magnitude of these vectors:

magnitude rx = 11.6 m

magnitude ry = 2.23 m - 0.99 m = 1.24 m

Then:

rx = (11. 6 m, 0)

ry = (0, -1.24 m)

r = (11.6 m + 0 m, 0 m - 1.24 m) = (11.6 m, -1.24 m)

Using trigonometry of right triangles:

magnitude rx = r * cos θ = 11. 6 m

magnitude ry = r * sin θ = 2.23 m - 0.99 = 1.24 m

where r is the magnitude of the vector r

magnitude of vector r:

`r = \sqrt{(11.6m)^(2) + (1.24m)^(2)} = 11.667m`

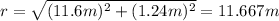
Then:

cos θ = 11.6 m / 11.667 m

θ = 6.1°

Using ry, we should obtain the same value of θ:

sin θ = 1.24 m/ 11.667 m

θ = 6.1°

( the exact value is obtained if we do not round the module of r)