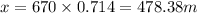Question

A Horizontal rifel is fired at a bull's-eye. The muzzle

speedof the bullet is 670 m/s. The barrel is pointed directly at
thecenter of the bull's-eye, but the bullet strikes the
target0.025m below the center. What is the horizontal distance
betweenthe end of the rifel and the bull's eye?

Answer 1

The horizontal distance is 478.38 m

Solution:

As per the question:

Initial Speed of the bullet in horizontal direction,
`v_(x) = 670 m/s`

Initial vertical velocity of the bullet,
`v_(y) = 0 m/s`

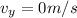
Vertical distance, y = 0.025 m

Now, for the horizontal distance, 'x':

We first calculate time, t:

`y = v_(y)t - (1)/(2)gt^(2)`

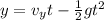
(since, motion is vertically downwards under the action of 'g')

`0.025 = 0 - (1)/(2)* 9.8t^(2)`

`t = √(0.05){9.8} = 0.0714 s`

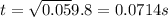
Now, the horizontal distance, x:

`x = v_(x)t + (1)/(2)a_(x)t^(2)`

`x = v_(x)t + (1)/(2)0.t^(2)`

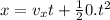
(since, the horizontal acceleration will always be 0)

`x = 670* 0.714 = 478.38 m`