Question

The output of an ac generator connected to an RLC series combination has a frequency of 12 kHz and an amplitude of 28 V. If R = 4.0 Ohms, L = 30 μH, and C = 8 μF, find a. The impedance

b. The amplitude for current
c. The phase difference between the current and the emf of the generator
Please show all steps and units. Thank you.

Answer 1

(a) 4.04 ohm

(b) 6.93 A

(c) 8.53°

Step-by-step explanation:

f = 12 kHz = 12000 Hz

Vo = 28 V

R = 4 ohm

L = 30 micro Henry = 30 x 10^-6 H

C = 8 micro Farad = 8 x 10^-6 F

(a) Let Z be the impedance

`X_(L) = 2\pi fL=2*3.14*12000*30*10^(-6)= 2.26 ohm`

`X_(c) = (1)/(2\pi fC)=(1)/(2*3.14*12000*8*10^(-6))= 1.66 ohm`

`Z = \sqrt{R^(2)+(X_(L)-X_(C))^(2)}=\sqrt{4^(2)+\left ( 2.26-1.66 \right )^(2)}`

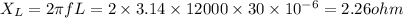
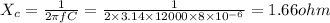
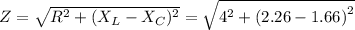
Z = 4.04 Ohm

(b) Let Io be the amplitude of current

`I_(o)=(V_(o))/(Z)`

`I_(o)=(28)/(4.04)`

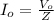
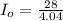
Io = 6.93 A

(c) Let the phase difference is Ф

`tan\phi = (X_(L)-X_(C))/(R)`

`tan\phi = (2.26-1.66)/(4)`

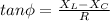
tan Ф =0.15

Ф = 8.53°