Answer:
a) The set of solutions is
 y b) the set of solutions is
y b) the set of solutions is
 .
.
Explanation:
a) Let's first find the echelon form of the matrix
![\left[\begin{array}{ccc}5&2&6\\-2&1&3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/jyszaupsny3utv4fq32pmonlj04o0halej.png) .
.
- We add
 from row 1 to row 2 and we obtain the matrix
from row 1 to row 2 and we obtain the matrix
![\left[\begin{array}{ccc}5&2&6\\0&(9)/(5) &(27)/(5)\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/acbk8l26y2c62libnmyw1yc4wzy98x36oq.png)
- From the previous matrix, we multiply row 1 by
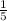 and the row 2 by
and the row 2 by
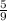 and we obtain the matrix
and we obtain the matrix
![\left[\begin{array}{ccc}1&(2)/(5) &(6)/(5) \\0&1&3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/dkfwhi3mxvjpyh6cyh442qg0t7col4odf6.png) . This matrix is the echelon form of the initial matrix.
. This matrix is the echelon form of the initial matrix.
The system has a free variable (x3).
- 0=x1+
 x2+
x2+
 x3=
x3=
x1+
 (-3x3)+
(-3x3)+
 x3=
x3=
x1-
 x3+
x3+
 x3
x3
then x1=0.
The system has infinite solutions of the form (x1,x2,x3)=(0,-3x3,x3), where x3 is a real number.
b) Let's first find the echelon form of the aumented matrix
![\left[\begin{array}{ccccc}1&-2&1&-4&1\\1&3&7&2&2\\0&-12&-11&-16&5\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/h3hnwc29dvnwck8zcme9rhvoxkb70rbsec.png) .
.
- To row 2 we subtract row 1 and we obtain the matrix
![\left[\begin{array}{ccccc}1&-2&1&-4&1\\0&5&6&6&1\\0&-12&-11&-16&5\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/1lejpdafkdpu1pbqvx00451v7k5uharbtk.png)
- From the previous matrix, we add to row 3,
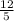 of row 2 and we obtain the matrix
of row 2 and we obtain the matrix
![\left[\begin{array}{ccccc}1&-2&1&-4&1\\0&5&6&6&1\\0&0&(17)/(5)&(-8)/(5)&(37)/(5) \end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/dq2xqbhhr6scfh7xteapi4ti384u8i7d8t.png) .
.
- From the previous matrix, we multiply row 2 by
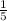 and the row 3 by
and the row 3 by
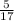 and we obtain the matrix
and we obtain the matrix
![\left[\begin{array}{ccccc}1&-2&1&-4&1\\0&1&(6)/(5) &(6)/(5)&(1)/(5)\\0&0&1&(-8)/(17)&(37)/(17) \end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/ioj3auglr04ykm4t4ecqc3cwu0v5ol0x7m.png) . This matrix is the echelon form of the initial matrix.
. This matrix is the echelon form of the initial matrix.
The system has a free variable (x4).
- x3-
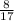 x4=
x4=
 , then x3=
, then x3=
 +
+
/(5)](https://img.qammunity.org/2020/formulas/mathematics/college/l1a6waadm0vvayadoenom9vk5za7bza575.png) x3+
x3+
 x4=
x4=
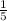 , x2+
, x2+
 (
(
 +
+
/(5)](https://img.qammunity.org/2020/formulas/mathematics/college/9y0z6rnp9gm2w4fvndx0v00zal5t162trn.png) x4=
x4=
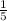 , then
, then
x2=
 x4.
x4.
- x1-2x2+x3-4x4=1, x1+
 +
+
 x4+
x4+
 +
+
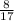 x4-4x4=1, then x1=
x4-4x4=1, then x1=
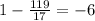
The system has infinite solutions of the form (x1,x2,x3,x4)=(-6,
 x4,
x4,
 +
+
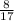 x4,x4), where x4 is a real number.
x4,x4), where x4 is a real number.